Digital Audio and the Mac
Fundamentals
Before we can discuss the specifics of digital sampling and synthesis, we need to ask some fundamental questions. What is sound? What causes us to perceive pitch, loudness, and timbre? How do we record and reproduce music? What are the differences between analog and digital recordings?
Sound
The phenomenon we call sound has three parts, all of which are necessary for its existence. First, a medium must be present that can transmit sound. This medium is usually air, but could also be water or a solid object, as sound passes through all three. Second, something must disturb this medium in order to create waves. These waves are generally alternations in air pressure, but they behave just as waves in water. Third, a receiver needs to be present in order to perceive the disturbance. The transmitter and receiver might be the same person, or two different individuals, but either way sound is perceived by anyone present.
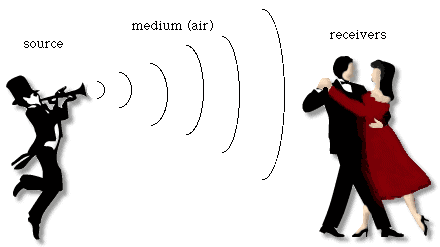
If any of these parts is absent, like an exploding TIE fighter in deep space (no air) or a tree falling in the forest (no one to hear it), there is no sound.
A Complex Phenomenon Simplified
All the sounds we hear are a complex mixture of waves, of all different sizes travelling in all different directions. Yet we only hear three things: frequency, amplitude, and phase. Frequency is dependent on the length of each wave. Since the speed of sound is constant within a given medium, then the shorter the wave, the higher the frequency. Amplitude is the literal strength of the wave measured in air pressure. The relationship can be shown easily by drawing a graph of amplitude over time.
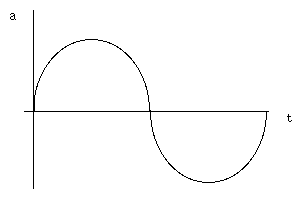
High and low pressure alternates at regular intervals, resulting in a simple periodic waveform (in this case, a sine wave). The length of the wave, 1/440 sec., also tells us the frequency indirectly. Since there are 440 cycles of pressure every second, we know the frequency is 440 Hz. The indicated amplitudes (1 and -1) simply indicate an arbitrary maximum and minimum.
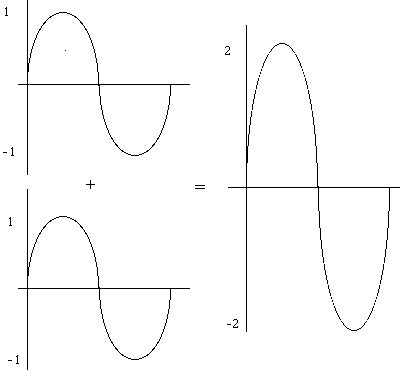
If we add a second wave at the same amplitude and frequency and begin both waves at exactly same time, they will reinforce each other and the result will be a doubling of amplitude. These waves are said to be ‘in phase.’ We can delay the onset of one wave, though, and shift it out of phase. In the extreme example, with the two waves 180° out of phase, they cancel each other out altogether.
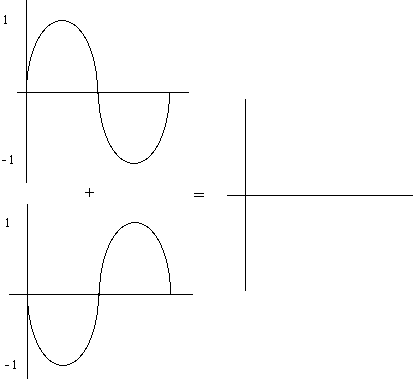
These examples are the clearest ones, but they never occur in nature. Waves are constantly cancelling and reinforcing parts of each other, but in much more complex ways. Not only are there many more than two waves present on most occasions, but the waves themselves are complex and contain many frequencies.
Partials
All natural sounds (and most artificial sounds, with one notable exception) are made up of multiple frequencies, each of which has a unique amplitude. These frequencies are called partials (partial frequencies). In the special case of musical notes, though, the partials have a particular “harmonic” relationship that allows us to perceive a unified pitch.

Some of you recognize this construction as the harmonic series. The frequencies are all related to the fundamental, or first harmonic, by whole number relationships. In this case, all the other waveforms will line up with the fundamental wave at each cycle, resulting in a clear pitch. Any time a number is doubled, it’s an octave. Other intervals are pure, and are approximated by the tempered scale (a discussion of tuning systems is way beyond the scope of this article—maybe later). The same structure exists in a piano note, a cello note, a bassoon note, etc. The amplitudes and phase relationships differ in every case, though, and these help us to distinguish between timbres.
Aside: Why Harmonics Instead of Overtones
The construct above is also referred to as the overtone series. I avoid the word overtone for the following reason: the overtone that determines the pitch is still called the fundamental, but it isn’t the first overtone. The frequency an octave higher is the first overtone, and the other overtones are numbered upward from there. It’s like stepping into an elevator in London (ok, a lift), pressing the button for the first floor and getting out one floor too high. Like a British lift, the overtone series has a ground floor that complicates matters. If I asked you “What’s the relationship between the 24th overtone and the 49th overtone?” you would just scratch your head, but if I asked you “What’s the relationship between the 25th harmonic and the 50th harmonic?” you would know immediately. They’re an octave apart.
Analog Recording
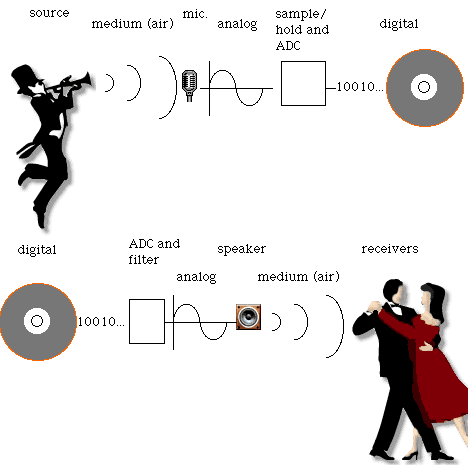
Before there were CDs and MiniDiscs and MP3s, there were LPs and cassette tapes. Even if you’ve long since parted with your record player, and haven’t used your cassette deck since you picked up that cool MP3 player, understanding how analog works is essential. It is still the intermediate step between you and your digital recording, and if you take it for granted you’ll regret it later. The term analog is short for analogous representation. The alternations in air pressure that we perceive as sound are transformed into analogous electrical voltages, sent up and down wires, through amplifiers and other components, and stored on magnetic tape. Let’s go back to our first diagram and add the analog stage.
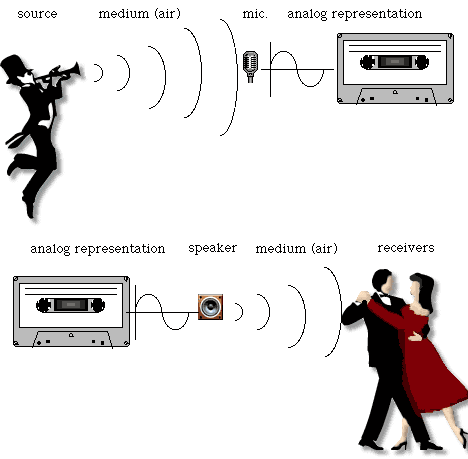
Transducers
In the diagram above, the microphone and the loudspeaker are the doors in and out of the analog world. Both are transducers: devices that change one kind of energy to another. The only difference between the two is the direction of the process.
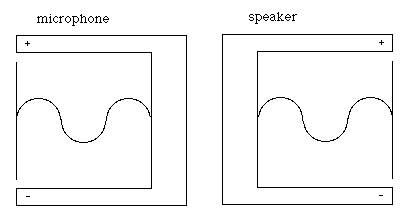
Have you ever used a set of headphones as a really cheap microphone? Now you know why it works. Each contains three parts, a membrane (diaphragm or speaker cone), a coil, and a magnet. The only difference is whether the membrane moves the coil or the coil moves the membrane. Well, that and the size. Loudspeakers are much larger than microphones because they have to handle much stronger signals. Next time you lift a speaker, remember that you’re only lifting a box, some paper, and a really big magnet.
Digital Recording
A digital recording is simply a series of numbers representing analog waveforms. The trick is in making the measurements. Since a continuous waveform can be measured at an infinite number of places, yet we can only make and store a finite number of measurements, the result will always be approximate. The trick is to make a lot of measurements at regular intervals.
What “Sampling” Really Means
The first step in making a digital representation is an analog component called a sample/hold generator. This device reads the continuous signal, and outputs fixed voltages at regular intervals. A strobe light is a good visual metaphor. The next step is an analog to digital converter (ADC), which measures each voltage output by the sample/hold generator. The measurements are output as binary data, which can then be stored on any appropriate medium. CDs, DAT tapes, and hard drives can store any kind of digital information including digital audio.
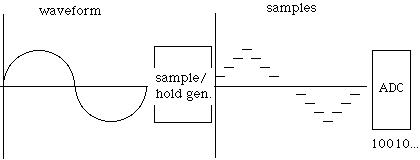
The Advantages of Digital
Once a signal enters the digital domain, it is simply a series of numbers. These numbers can be transferred between media repeatedly without degradation. Tape, on the other hand, accumulates noise with each generation. The other advantage is flexibility. Digital audio can be easily edited on a hard drive. It can also be modified in any way that can be mathematically modelled. A sound source can be placed in a bathroom, a gymnasium, or the Taj Mahal just by pressing a few buttons.
Digital Reproduction
No matter how you manipulate them, though, they’re still numbers. At some point the sound must be reconstructed out of all those numbers. A digital to analog converter (DAC) produces voltages for each number. As long as the DAC and the ADC run at the same rate (like a movie camera and a projector must run at the same rate), the original wave is reproduced. Well, not quite. Just as a sample/hold generator is needed to break up a continuous signal, a low pass filter (more on filters next month) smooths out the digital stairsteps.
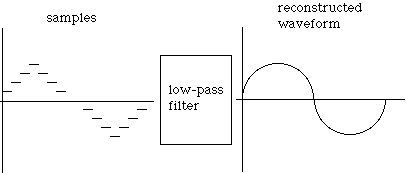
Put all the pieces together, and it looks like this.
Next month: Digital Audio and the Mac—Part Two: The Specifics of Sampling.
Also in This Series
- Digital Audio on the Internet · June 2000
- Hardware · May 2000
- Software · April 2000
- The Specifics of Sampling · March 2000
- Fundamentals · February 2000
- Complete Archive
Reader Comments (7)
So your shareware may not be windowing your audio signals in a "natural" way. That is, not the way your ears and brain perceive that signal. The window spacing, shape, and length all contribute here. Incidentally, the Gabor transform (or short time Fourier transform) is the appropriate mathematical analysis tool to use here.
My best guess is that the windows are spaced too far apart for the given window size/shape.
Add A Comment